트리
힙과 우선순위 큐가 트리 형태로 이루어져있기 때문에 어느정도 알고 있어야한다.
트리란? 계층적 구조를 갖는 데이터를 표현하기 위한 자료구조이다. 노드와 간선으로 이루어져있다.
이것만 보면 그래프와 매우 유사한 형태를 가지고 있다.
트리와 그래프의 큰 차이는 트리는 계층 구조를 가지는 것이다. 그래프는 동등한 위치의 데이터들을 간선으로 이은 것이라 할 수 있다.

제일 중요한 것은 root와 leaf이다.
간단하게 코드로 나타내보자.
#include <iostream>
#include <vector>
#include <list>
#include <stack>
#include <queue>
using namespace std;
using NodeRef = shared_ptr<struct Node>;
struct Node
{
Node() { }
Node(const string& data) : data(data) { }
string data;
vector<NodeRef> Children;
};
NodeRef CreateTree()
{
NodeRef root = make_shared<Node>("R1 개발실");
{
NodeRef node = make_shared<Node>("디자인 팀");
root->Children.push_back(node);
{
NodeRef leaf = make_shared<Node>("전투");
node->Children.push_back(leaf);
}
{
NodeRef leaf = make_shared<Node>("경제");
node->Children.push_back(leaf);
}
{
NodeRef leaf = make_shared<Node>("스토리");
node->Children.push_back(leaf);
}
node = make_shared<Node>("프로그래머 팀");
root->Children.push_back(node);
{
NodeRef leaf = make_shared<Node>("서버");
node->Children.push_back(leaf);
}
{
NodeRef leaf = make_shared<Node>("클라");
node->Children.push_back(leaf);
}
{
NodeRef leaf = make_shared<Node>("엔진");
node->Children.push_back(leaf);
}
node = make_shared<Node>("아트 팀");
root->Children.push_back(node);
{
NodeRef leaf = make_shared<Node>("배경");
node->Children.push_back(leaf);
}
{
NodeRef leaf = make_shared<Node>("캐릭터");
node->Children.push_back(leaf);
}
}
return root;
}
void PrintTree(NodeRef root, int depth)
{
for (int i = 0; i < depth; i++)
{
cout << "-";
}
cout << root->data << endl;
for (NodeRef& child : root->Children)
{
PrintTree(child, depth +1);
}
}
// 깊이(depth) : 루트에서 어떤 노드에 도달하기 위해 거쳐야하는 간선의 수(aka. 몇 층?)
// 높이(height) : 가장 깊숙히 있는 노드의 깊이(max(detph))
int GetHeight(NodeRef root)
{
int height = 1;
for (NodeRef& child : root->Children)
{
height = max(height, GetHeight(child) + 1);
}
return height;
}
int main()
{
NodeRef node = CreateTree();
PrintTree(node, 0);
int height = GetHeight(node);
cout << height;
}Heap
이진 트리란 무엇인가? 각 노드가 최대 두 개의 자식 노드를 가지는 트리를 말한다. 이진 트리를 왜 사용하는가? 어떤 데이터를 검색하는데 유용하게 사용된다. 왼쪽을 타고 가면 현재 값보다 작은 숫자가 존재하고 오른쪽을 타고 가면 현재 값보다 크게 배치를 해 빠르게 데이터를 찾을 수 있다.
그에비해 힙 트리는 살짝 다르다.
힙 트리에는 중요한 규칙이 있다. 첫 번째로 부모 노드가 가진 값은 항상 자식 노드가 가진 값보다 크다는 것이다.
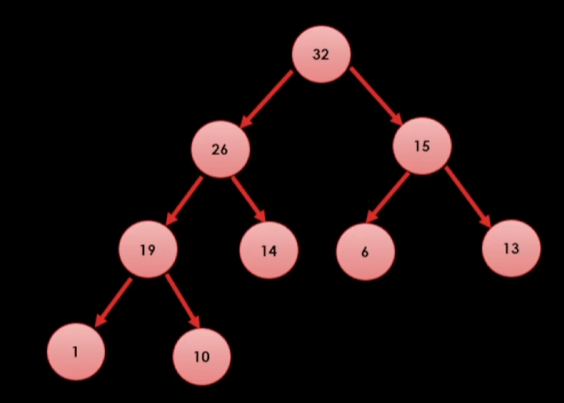
두 번째로 노드 개수를 알면, 트리 구조는 무조건 확정할 수 있다.
왜냐하면 마지막 레벨을 제외한 모든 레벨에 노드가 꽉 차있다게 배치를 해야하고, 마지막 레벨에 노드가 있을 때는, 항상 왼쪽부터 순서대로 채워야하는 규칙에 따르면 트리 구조를 무조건 확정 할 수 있다.
값을 추가하는 방식은 맨 뒤에 값을 추가하고 도장깨기를 통해 앞으로 전진하다.
또, 최대값을 찾을 때는 맨위의 노드 즉, root를 추출하면 된다. 그리고 맨 뒤에 있는 노드를 root에 놓고 역으로 도장깨기를 하면 된다. 이 동작 방식을 꼭 알고 있자.
우리가 다루고자 하는 건 우선순위 큐인데 이는 힙트리로 이루어져 있다.
우선순위 큐 구현
#include <iostream>
#include <vector>
#include <list>
#include <stack>
#include <queue>
using namespace std;
template<typename T, typename Container = vector<T>, typename Predicate = less<T>>
class PriorityQueue
{
public:
void push(const T& data)
{
// 우선 힙 구조부터 맞춰준다.
_heap.push_back(data);
// 도장깨기 시작
int now = static_cast<int>(_heap.size()) - 1;
// 루트 노드까지
while (now > 0)
{
// 부모 노드의 데이터와 비교해서 더 작으면 패배
int next = (now - 1) / 2;
if (_predicate(_heap[now], _heap[next]))
break;
// 데이터 교체
::swap(_heap[now], _heap[next]);
now = next;
}
}
void pop()
{
_heap[0] = _heap.back();
_heap.pop_back();
int now = 0;
while (true)
{
int left = 2 * now + 1;
int right = 2 * now + 2;
// 리프에 도달한 경우
if (left >= _heap.size())
break;
int next = now;
// 왼쪽과 비교
if (_predicate(_heap[next], _heap[left]))
next = left;
// 둘 중 승자를 오른쪽과 비교
if (right < (int)_heap.size() && _predicate(_heap[next], _heap[right]))
next = right;
// 왼쪽 오른쪽 둘다 현재 값보다 작으면 종료
if (next == now)
break;
swap(_heap[now], _heap[next]);
now = next;
}
}
T& top()
{
return _heap[0];
}
bool empty()
{
return _heap.empty();
}
private:
Container _heap = {};
Predicate _predicate;
};
int main()
{
PriorityQueue<int, vector<int>, std::greater<int>> pq;
pq.push(900);
pq.push(200);
pq.push(120);
pq.push(400);
pq.push(700);
while (pq.empty() == false)
{
int value = pq.top();
pq.pop();
cout << value << endl;
}
}A* 길찾기 알고리즘
우리가 지금까지 미로게임을 구현할 때, 목적지를 정해준 적은 없었다. 계속 앞으로 나가아다가 목적지에 도달하면 break를 통해 멈추는 형식이었다. 그 방식이 아닌 스타크래프트 처럼 시작점과 목적점을 정확히 지정해 이동하는 방식이다.
시작점에서 얼마나 떨어져 있냐, 도착점에서 얼마나 떨어져 있냐 이 2가지의 점수를 매겨 제일 좋은 길을 고르는 것이다.
#include "pch.h"
#include "Player.h"
#include "Board.h"
#include <stack>
void Player::Init(Board* board)
{
//int a;
//cin >> a;
_pos = board->GetEnterPos();
_board = board;
// RightHand();
//Bfs();
Astar();
}
void Player::Update(uint64 deltaTick)
{
if (_pathIndex >= _path.size())
{
_board->GenerateMap();
Init(_board);
return;
}
_sumTick += deltaTick;
if (_sumTick >= MOVE_TICK)
{
_sumTick = 0;
_pos = _path[_pathIndex];
_pathIndex++;
}
}
bool Player::CanGo(Pos pos)
{
TileType tileType = _board->GetTileType(pos);
return tileType == TileType::EMPTY;
}
void Player::RightHand()
{
Pos pos = _pos; // 임시
_path.clear();
_path.push_back(pos);
//목적지 도착하기 전에는 계속 실행
Pos dest = _board->GetExitPos();
Pos front[4] = {
Pos {-1, 0}, // up
Pos {0 , -1}, // left
Pos {1, 0}, // down
Pos {0, 1}, // right
};
while (pos != dest)
{
// 1. 현재 바라보는 방향을 기준으로 오른쪽으로 갈 수 있는지 확인
int32 newDir = (_dir - 1 + DIR_COUNT) % DIR_COUNT;
if (CanGo(pos + front[newDir]))
{
// 오른쪽 방향으로 90 회전.
_dir = newDir;
// 앞으로 한 보 전진
pos += front[_dir];
_path.push_back(pos);
}
// 2. 현재 바라보는 방향으로 기준으로 전진할 수 있는지 확인.
else if (CanGo(pos + front[_dir]))
{
// 앞으로 한보 전진.
pos += front[_dir];
_path.push_back(pos);
}
else
{
// 왼쪽 방향으로 90도 회전.
_dir = (_dir + 1) % DIR_COUNT;
}
}
stack<Pos> s;
for (int i = 0; i < _path.size() - 1; i++)
{
if (s.empty() == false && s.top() == _path[i + 1])
s.pop();
else
s.push(_path[i]);
}
// 목적지 도착
if (_path.empty() == false)
s.push(_path.back());
vector<Pos> path;
while (s.empty() == false)
{
path.push_back(s.top());
s.pop();
}
std::reverse(path.begin(), path.end());
_path = path;
}
void Player::Bfs()
{
Pos pos = _pos; // 임시
//목적지 도착하기 전에는 계속 실행
Pos dest = _board->GetExitPos();
Pos front[4] = {
Pos {-1, 0}, // up
Pos {0 , -1}, // left
Pos {1, 0}, // down
Pos {0, 1}, // right
};
// 발견 여부
const int32 size = _board->GetSize();
//vector<vector<bool>> discovered(size, vector<bool>(size, false));
map<Pos, bool> discovered;
// vector<vector<Pos>> parent;
// parent[A] = B; -> A는 B로 인해 발견함.
map<Pos, Pos> parent;
queue<Pos> q;
q.push(pos);
//discoverd[pos.y][pos.x] = true;
discovered[pos] = true;
parent[pos] = pos;
while (q.empty() == false)
{
pos = q.front();
q.pop();
// 방문
if (pos == dest)
break;
for (int32 dir = 0; dir < 4; dir++)
{
Pos nextPos = pos + front[dir];
// 갈 수 있는 지역인지 확인
if (CanGo(nextPos) == false)
continue;
// 이미 발견한 지역인지 확인
if (discovered[nextPos])
continue;
q.push(nextPos);
discovered[nextPos] = true;
parent[nextPos] = pos;
}
}
_path.clear();
// 거꾸로 거슬러 올라가기
pos = dest;
while (true)
{
_path.push_back(pos);
if (pos == parent[pos])
break;
pos = parent[pos];
}
reverse(_path.begin(), _path.end());
}
struct PQNode
{
PQNode(int32 f, int32 g, Pos pos): f(f), g(g), pos(pos){ }
bool operator<(const PQNode& other) const { return f < other.f; }
bool operator>(const PQNode& other) const { return f > other.f; }
int32 f;
int32 g;
Pos pos;
};
void Player::Astar()
{
// 점수 매기기
// F = G + H
// F = 최종 점수(작을 수록 좋음, 경로에 따라 달라짐)
// G = 시작점에서 해당 좌표까지 이동하는데 드는 비용(작을 수록 좋음)
// H = 목적지에서 얼마나 가까운지 (작을 수록 좋은, 고정)
Pos start = _pos; // 시작점
Pos dest = _board->GetExitPos(); // 목적지
enum
{
DIR_COUNT = 8,
};
Pos front[] = {
Pos {-1, 0}, // up
Pos {0 , -1}, // left
Pos {1, 0}, // down
Pos {0, 1}, // right
Pos {-1, -1}, // up + left
Pos {1, -1}, // down + left
Pos {1, 1}, // down + right
Pos {-1, 1}, // up + right
};
int32 cost[] {
10, // up
10, // left
10, // down
10, // right
14, // up + left
14, // down + left
14, // down + right
14 // up + right
};
const int32 size = _board->GetSize();
// ClosedList
// close[y][x] -> (y,x)에 방문 했는지 여부
vector<vector<bool>> closed(size, vector<bool>(size, false));
// best[y][x] -> 지금까지 (y,x)에 대한 가장 좋은 비용(작을 수록 좋음)
vector<vector<int32>> best(size, vector<int32>(size, INT32_MAX));
// 부모 추적 용도
map<Pos, Pos> parent;
// 1) 예약(발견) 시스템 구현
// 2) 뒤늦게 더 좋은 경로가 발견될 수 있음 -> 예외처리 필수
priority_queue<PQNode, vector<PQNode>, greater<PQNode>> pq;
{
int32 g = 0;
// 우리가 마음대로 만드는 것
int32 h = 10 * (abs(dest.y - start.y) + abs(dest.x - start.x));
pq.push(PQNode(g + h, g, start));
best[start.y][start.x] = g + h;
parent[start] = start;
}
while (pq.empty() == false)
{
// 제일 좋은 후보를 찾는다.
PQNode node = pq.top();
pq.pop();
// 동일한 좌표를 여러 경로를 찾아서
// 더 빠른 경로로 인해 이미 방문이 된 경우 스킵
// [선택] 밑의 둘 중 하나 선택
if (closed[node.pos.y][node.pos.x])
continue;
if (best[node.pos.y][node.pos.x] < node.f)
continue;
// 방문
closed[node.pos.y][node.pos.x] = true;
// 목적지에 도착햇으면 종료
if (node.pos == dest)
break;
for (int32 dir = 0; dir < DIR_COUNT; dir++)
{
Pos nextPos = node.pos + front[dir];
// 갈수 있는 지역은 맞는지 확인
if (CanGo(nextPos) == false)
continue;
// [선택] 이미 방문한 곳이면 스킵
if (closed[nextPos.y][nextPos.x])
continue;
// 비용 계산
int32 g = node.g + cost[dir];
int32 h = 10 * (abs(dest.y - nextPos.y) + abs(dest.x - nextPos.x));
// 다른 경로에서 더 빠른 길을 찾았으면 스킵
if (best[nextPos.y][nextPos.x] <= g + h)
continue;
best[nextPos.y][nextPos.x] = g + h;
pq.push(PQNode { g + h,h,nextPos });
parent[nextPos] = node.pos;
}
}
Pos pos = dest;
_path.clear();
_pathIndex = 0;
// 거꾸로 거슬러 올라가기
pos = dest;
while (true)
{
_path.push_back(pos);
if (pos == parent[pos])
break;
pos = parent[pos];
}
reverse(_path.begin(), _path.end());
}'C++ > 알고리즘' 카테고리의 다른 글
| [C++ algorithm] 각종 정렬에 대해 (0) | 2023.12.14 |
|---|---|
| [C++ algorithm] 이진 탐색 트리, 레드 블랙 트리 (0) | 2023.12.13 |
| [C++ algorithm] 그래프, BFS, DFS (0) | 2023.12.09 |
| [C++ algorithm] 스택, 큐, 오른손 법칙 개선 (1) | 2023.12.08 |
| [C++ algorithm] 배열, 동적배열, 연결리스트 (1) | 2023.12.08 |
