행렬 기초
행렬을 처음 이해할 때, 하나의 포탈이라고 이해하면 편하다.

만약 어떤 물체가 Scale이라는 행렬 포탈안에 들어가게 된다면 물체의 Scale이 조정이 되는 것이다. 만약 Rotation에 들어가게 된다면 회전을 하게되는 것이다.
즉, 하나의 변화를 나타낸다 라는 개념으로 이해하면 된다.(게임에서)
행렬은 말 그대로 행(Row)과 열(Col)로 이루어진 수식을 의미한다.
3개의 행이 있고 2개의 열이 있다면 3x2 행렬이라고 말한다.
그리고 1행 1열 1행 2열 순으로 번호를 매긴다.

행렬에 대한 특징으로 행렬 M에 k를 곱하면 각 요소에 전부 다 k를 곱하는 특성을 가지고 있다.

행렬의 덧셈 뺄셈은 각 위치끼리 더하고 빼기를 하게된다. 하지만 유의해야할 점은 행렬의 사이즈가 동일해야한다는 점이다.

가장 중요한 점은 행렬의 곱셈이다. 행렬의 곱셈의 조건은 곱셈을 하는 주체의 열과 행의 크기가 똑같아야만 한다.

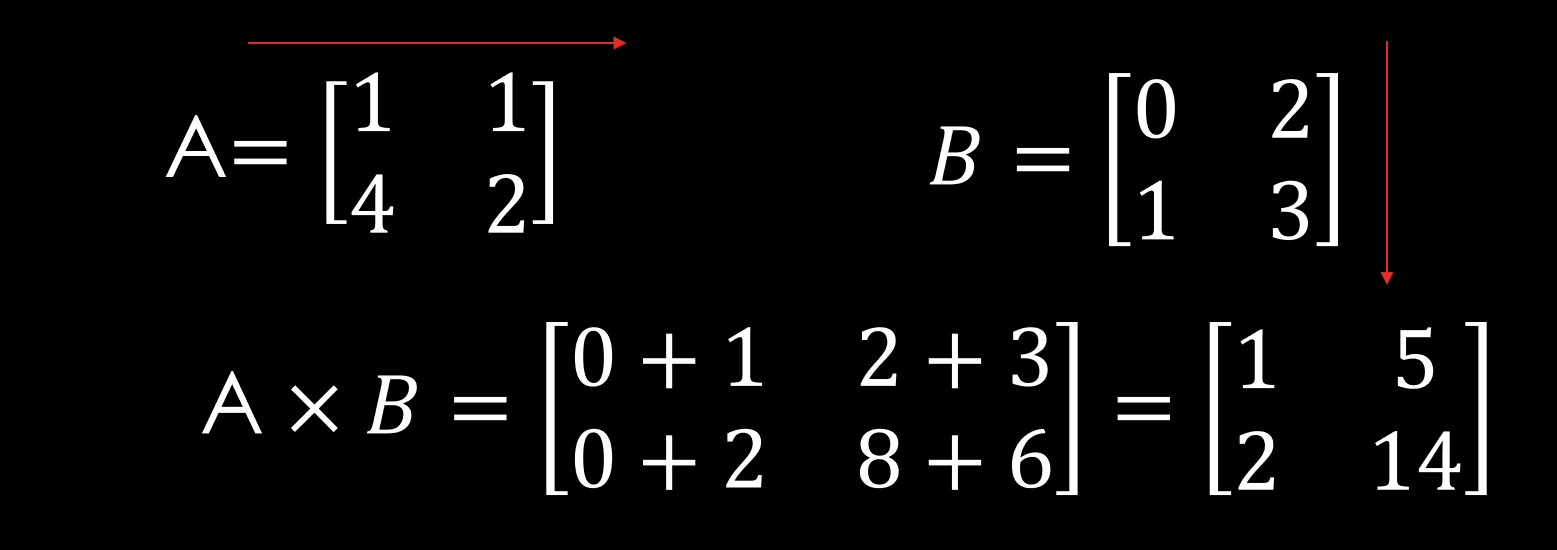
1열 1행만 예시를 들자면 1*0 + 1 *1 = 0 + 1 인 것이다.
위에서 말한 포탈들을 동시에 사용하기 위해 쓰는 것이 바로 곱셈이기 때문에 매우 중요하다고 할 수 있다. 개념적으로 한번만 읽히면 그 뒤로는 코드를 짜서 하기 때문에 매번 손으로 계산할 필요는 없다.
그렇다면 A * B가 B * A가 동일할까? 당연히 안된다.
앞에 오는 행렬의 열과 뒤에 오는 행렬의 행의 크기가 똑같아야 할 수 있는데 순서가 뒤바뀌면 곱셈이 틀어진다.
행렬을 변화로 예시를 들었는데 만약 M * A * B = M 이라면 M에다가 A라는 변화를 주고 B라는 변화를 연속해서 줬는데 다시 제자리로 돌아왔다는건 A와 B가 서로 상쇄할만한 변화를 가지고 있다는 것이다.
이때 B를 A의 역행렬 이라고 한다.
우리가 어떤 변화를 줬다가 다시 취소하고 싶을 때 주로 사용하기에 많이 사용하게 될 것이다.

역행렬이 항상 존재하진 않지만 D를 구하면 있는지 없는지를 확인할 수 있다.
역행렬을 구하는 방식이 차원이 넓어지면 매우 복잡해지는데 분명 연습할 필요가 있다.
이 내용은 수학 책을 펼쳐보면 다 알 수 있는 내용이다.
우리한테 중요한 것은 "그래서 행렬을 배웠는데 어디다가 쓰는건데?" 이다.
우리는 게임에서 좌표를 표현할 때 벡터를 이용한다. x y z를 벡터를 하나의 행렬로 표현하고 이를 "변화"하고 싶을 때 행렬의 곱을 이용하는 것이다.
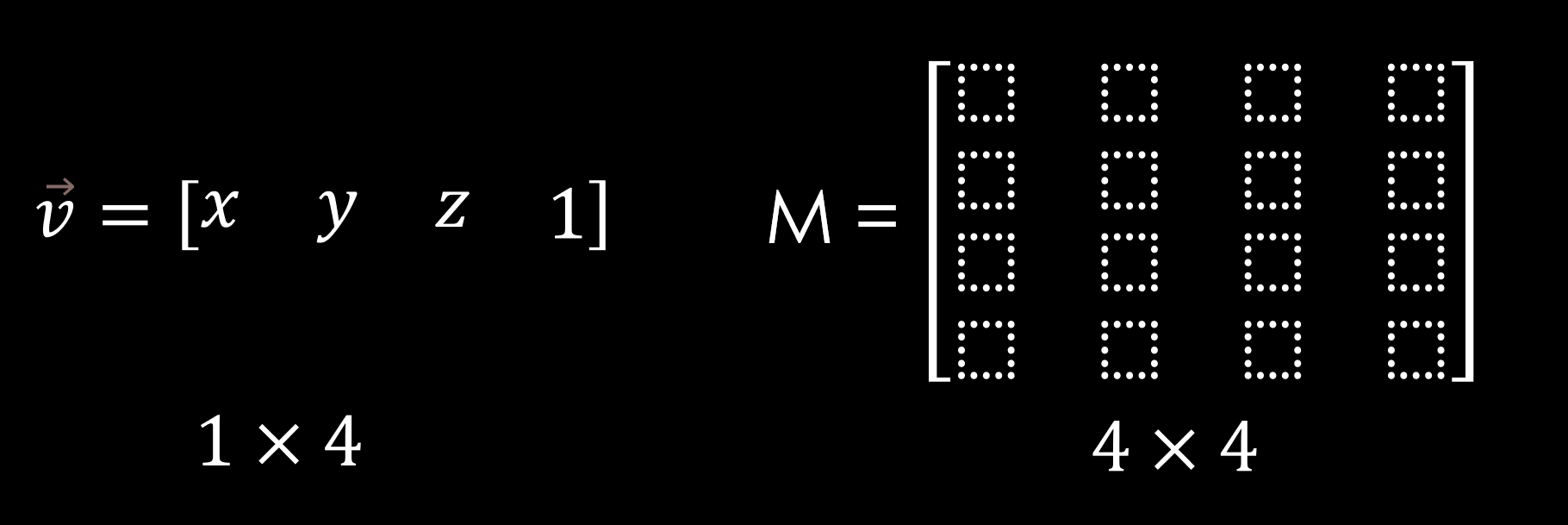
만약 게임에서 특정 좌표에 있을 때 , M 이라는 포탈을 타게되면 좌표가 어떻게 변할까 등을 나타내는 것이다.

SRT 변환 행렬
첫번째로 T : Translation에 대해 알아보자.
어떤 물체가 x,y,z 의 좌표를 가지고 3차원 공간안에 있을 때, 평행이동을 하고 싶다고 해보자.
x,y,z가 벡터였다면 우리가 이동하고자 하는 X,Y,Z는 방향벡터 a,b,c를 구해서 x,y,z에 더해줬으면 됐을 것이다.

그렇다면 행렬로 하려면 어떻게 해야할까?? 즉, m을 채워야 하는 것이다.
행렬의 곱을 생각해서 M을 채우는데 어떻게 해도 x + a는 나오지 않는다. X는 xm11 + ym21 + zm32 일 텐데 이게 x+a가 되려면 y와 z가 0이 되어야하고 m11은 1이 되어야한다. 어떻게 하든 a가 나올 구멍이 없는 것이다.
그렇기 때문에 강제로 4차원으로 만들어 동차 좌표계를 이용한다.

이렇게 하면 Translation 포탈이 생성되는 것이다. 현재 위치의 벡터와 이동하고자하는 위치벡터만 있다면 우리는 목적지까지 바로 구할 수 있다.
S : Scale은 더욱 간단하다.
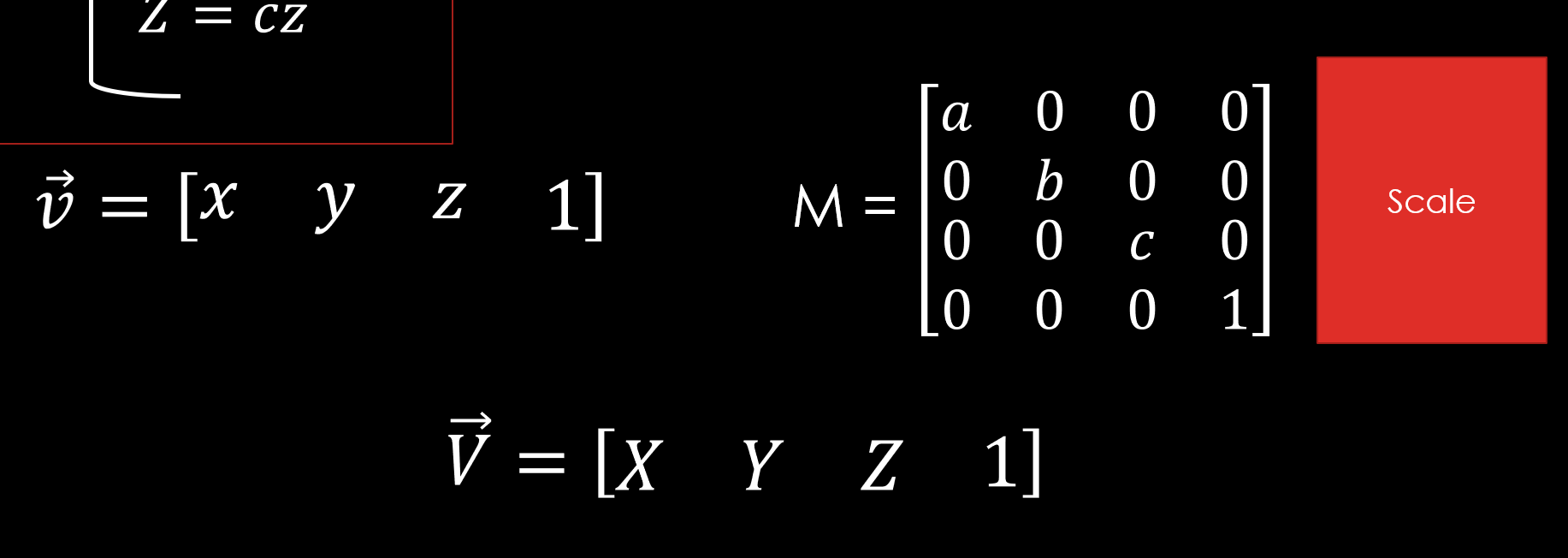
단순히 a b c만 채우면 되기 때문이다. 이것이 Scale 포탈이다.
R : Rotation은 단순하지 않다.
회전은 특정 축을 먼저 설정해야하는데 선택된 축은 움직이지 않고 나머지가 회전한다는 뜻이다. 즉, 선택된 축을 기준으로 회전하는 것이다.
만약 z축을 기준으로 x,y 좌표에서 X,Y 좌표로 이동한다고 해보자.

삼각 함수를 이용해서 새로운 X, Y 좌표를 추출해낼 수 있는데 이걸 행렬을 통해 값을 얻어내기 위해선 어떤 M 값을 넣어야할지 생각해보자.

이건 z축을 기준으로 회전할 때 공식인 것이고
최종적으로는 다음과 같다.

이제 이 세가지의 행렬을 하나로 합쳐서 우리는 SRT 변환 행렬을 만들 것이다.
그 때 반드시 기억해야하는 것은 "스 자 이 공 부" 이다.
스케일
자전
이동
공전
부모행렬
반드시 이 순서대로 곱해야한다.

왜 그래야만 할까??
첫번째 연산이 두번째 연산에 영향을 주기 때문에 그 영향이 없게하기 위해 순서를 정해놓은 것이다.
좌표계 변환 행렬
이번에 알아볼 것은 좌표계를 행렬을 통해 변환하는 것이다. 렌더링 과정중 VS 과정에서 우리는 오브젝트의 로컬 좌표에서 월드 좌표로 또 월드 좌표에서 카메라 좌표로 등 우리가 화면에 물체를 보여주기 위해 좌표계를 계속 수정해야만 한다.
어떻게 변환하는지 알아보자.
A라는 좌표에서 M이라는 좌표를 벡터를 이용해 나타내면 다음과 같다.

그런데 만약 새로운 좌표 B를 기준으로 하면 어떻게 표현할까? 아래 처럼 표현할 수 있다.

그런데 문제가 있다. 대부분의 경우 우리는 X, Y, V, U를 아는 상황보다 모르는 상황이 훨씬 많다.
즉 x,y, u, v만 알고 있을 때는 어떻게 표현할까??

이 수식에서 ux와 uv는 기존 u,v 단위 벡터를 U,V 단위 벡터의 기준으로 쪼갠 어떠한 값이다.
이 값들을 행렬로 나타내보면

이 행렬이 만능 공식이다. 아직 와닿지 않을 수 있는데,
분석을 해보자면
우리는 A 좌표계에서 새로운 기준점인 B로 변환하고 하는 것이고, B 좌표계를 기준으로 했을 때, A의 단위 벡터인 u,v,w의 성분을 변환한 것이 ux, uy, uz... 인것이고 B좌표계를 기준으로 A의 좌표가 Qx,Qy,Qz 인 것이다.

가령 어떤 물체가 A 좌표계 기준으로 3,5에 있었는데 B 좌표계를 기준으로 변환하고 싶다면. 위의 표를 한번만 채운 다음 3,5를 행렬 변환을 통해 B 기준 좌표계로 1,2 등으로 변환할 수 있게 된 것이다.
예제
우리가 하고자 하는건 오브젝트마다 고유의 좌표계를 가지고 있는데 그것을 화면에 보여주기 위해 좌표계를 다음과 같이 수정하는 것이 목표이다.
로컬 좌표계 <-> 월드 좌표계 <-> 뷰 좌표계 <-> 투영 좌표계 <-> 스크린 좌표계
어떤 오브젝트를 카메라 안 화면에 보여주기 위해서는 위의 과정이 필요하다.
코드로 보면 이해가 쉽다.
이전 포스팅에서 이미지를 움직이는 것을 update 마다 offset을 추가 설정해 이미지를 움직였었는데 그 방식이 아니라 실제로 행렬을 이용해 처리하면 다음과 같다.
void Game::Update()
{
// Scale Rotation Translation
_localPosition.x += 0.001f;
Matrix matScale = Matrix::CreateScale(_localScale / 3);
Matrix matRotation = Matrix::CreateRotationX(_localRotation.x);
matRotation *= Matrix::CreateRotationY(_localRotation.y);
matRotation *= Matrix::CreateRotationZ(_localRotation.z);
Matrix matTranslation = Matrix::CreateTranslation(_localPosition);
Matrix matWorld = matScale * matRotation * matTranslation; // SRT
_transformData.matWorld = matWorld;
D3D11_MAPPED_SUBRESOURCE subResource;
ZeroMemory(&subResource, sizeof(subResource));
_deviceContext->Map(_constantBuffer.Get(), 0, D3D11_MAP_WRITE_DISCARD, 0, &subResource);
::memcpy(subResource.pData, &_transformData, sizeof(_transformData));
_deviceContext->Unmap(_constantBuffer.Get(), 0);
}스 자 이(순서를 반드시 지키며) 행렬을 만들어 서로를 곱해주면 그 정보를 월드 행렬을 얻을 수 있다.
이를 constantBuffer에 저장한 후 Data를 쉐이더에 넘겨주게 되면 VS 과정에서 다음과 같이 작동한다.
VS_OUTPUT VS(VS_INPUT input)
{
VS_OUTPUT output;
// WVP
float4 position = mul(input.position, matWorld); // W
position = mul(position, matView); // V
position = mul(position, matProjection); // P
output.position = position;
output.uv = input.uv;
return output;
}월드 행렬을 로컬 좌표에 곱해서 월드 좌표계로 변환 후 그 값을 다시 뷰 좌표계, 투영 좌표계를 곱해서 값을 얻어내면 최종 결과물이 되는 것이다. 물론 이 경우에는 뷰 좌표계랑 투영 좌표계는 항등행렬이다.

'C++ > DirectX 11' 카테고리의 다른 글
| [DirectX] 프레임워크 제작기 - Shader, Pipeline, GameObject (1) | 2024.09.03 |
|---|---|
| [DirectX] 프레임워크 제작기 - Graphics, IA, Geomotry (1) | 2024.09.02 |
| [DirectX] DirectX 11 입문하기 - Constant Buffer와 State (0) | 2024.08.29 |
| [DirectX] DirectX 11 입문하기 - 텍스쳐와 UV (3) | 2024.08.28 |
| [DirectX] DirectX 11 입문하기 - 장치 초기화와 삼각형 띄우기 (0) | 2024.08.28 |
